2011
| News | Registration | Abstract submission | Deadlines | Excursions | Accommodation | Organizing committee |
| First circular | Second circular | Abstracts | Seminar History | Program | Travel | Contact us |
| Новости |
| Первый циркуляр |
| Второй циркуляр |
| Регистрация |
| Оформление тезисов |
| Тезисы |
| Программа |
| Участники |
| Размещение |
| Экскурсии |
| Проезд |
| Важные даты |
| Оргкомитет |
| Обратная связь |
Тезисы международной конференции
Abstracts of International conference
The reasons of kimberlite occurrences clustering
Y. M. Khazan, O. V. Aryasova
S.I.Subbotin Institute of geophysics, Kiev, Ukraine
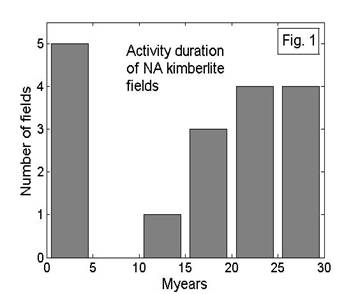
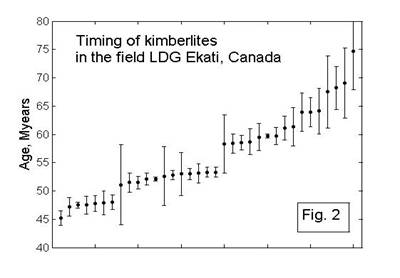
A significant characteristic of processes inside kimberlite sources is duration of their activity. The data for North America [Heaman et al., 2004] suggest an existence of two intervals of kimberlite fields activity duration of 1 to 3 Myears, and 17 to 30 Myears with a large gap between them (Fig. 1). A more detailed study of the kimberlite timing for the fields where many kimberlite age determinations are known (LDG Ekati, Lac de Gras, Kirkland Lake) shows that ages combine into compact groups with a scatter inside a group not exceeding a measurement error of 1 to 3 Myears. An example is shown in Fig. 2. One can see from the figure that 35 age determinations for the LDG Ekati field may be subdivided into 5 groups. Three of them are well defined (7 ages in the range of 45.2 to 48 Myears, 12 ages in the range of 51.1 to 53.3 Myears, and 9 ages in the range of 58.3 to 61.3 Myears). Two others are not well expressed and contain three or four age determinations close to 64 and 68 Myears. These data allow to conclude that clusters of approximately same age kimberlites include several (up to 10—12) eruptions occurring during a time interval of the order of a few million years. The kimberlites in a cluster have approximately same composition and form a close space group [Vaganov, 2000]. The second time scale of 10 to 30 Myears recorded also in the Yakutian kimberlite province [Ukhanov et al., 1988] corresponds to a lifetime of a field during which a few clusters form.
High abundances of incompatible elements in kimberlites are indicative of low (~1%) or even infinitesimal (~0.1%) melting degree in a source. This means that initially the protokimberlite melts exist as a system of dispersed small inclusions while the kimberlite transportation to the surface assumes existence of macroscopic melt pools. In other words, an inevitable stage of the protokimberlite melt evolution is its segregation from the porous matrix inside a partially molten zone and accumulation in a region where the melt fraction greatly exceeds the initial melting degree. Khazan [2010] and Khazan, Aryasova [2011] demonstrated that if the system of melt inclusions is interconnected, the characteristic segregation time, τ, depends on the ratio of the molten zone thickness, L, to the compaction length, δ, which in its turn is defined by the viscosities of the melt, μ, and matrix, η, and the matrix permeability. In the limiting case L/δ<10 (low viscosity melts) the segregation time decreases with increasing molten zone thickness τ≈19.5(η/∆ρgL) and is independent of poorly known melt viscosity and matrix permeability. The latter implies that the low viscosity melt segregation time does not depend on the melting degree as well.
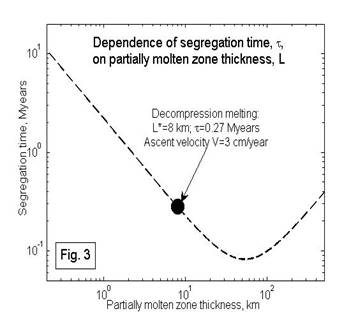
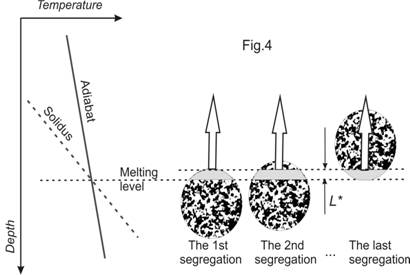
The decreasing dependence of the segregation time on the molten zone thickness constrains the latter and is the reason of the formation of clusters of approximately same age and composition eruptions. To illustrate, assume that the melting is due to decompression and accompanies an ascent of a mantle diapir with a velocity V. In this case the molten zone thickness increases linearly with time L=Vt where the time t is measured from the moment when the diapir top reaches the solidus level. Since no system can exist longer than its decay time is, the time t cannot exceed the segregation time t≤τ, wherefrom L≤L*=4.4(Vη/∆ρg)1/2. Under a robust parameter values choice (η=1019 Pa s, ∆ρ=300 kg/m3, V=3 cm/year) the segregation occurs when the molten zone thickness reaches about 8 km, with the corresponding segregation time τ being of 0.27 млн. лет. The condition of the estimate applicability (L*/δ<10) is satisfied because the compaction length, δ, is of 6 km. After the first segregation, a new partially molten zone grows resulting in the next segregation when its thickness reaches its maximum possible value L*. This sequence of events repeats until the whole diapir passes by the melting level. One may estimate the diapir diameter D=30 to 80 km based upon a size of low amplitude uplifts associated with the kimberlite fields (e. g., Kaminsky et al. [1995], Vaganov [2000]). So the diapir ascent results in formation of an eruption cluster consisting of D/L*=3—10 eruptions during the time of τD/L*=1—3 Myears as it is really observed. The described sequence of events is schematically illustrated in Fig, 4.
References
Heaman L., Kjarsgaard B., Creaser R. The temporal evolution of North American kimberlites // Lithos. 2004. V. 76. P. 377—397.
Vaganov V. I. The diamond deposits of the world and Russia. Moscow: Geoinformmark. 2000. — 371 p. (In Russian)
Ukhanov A. V., Ryabchikov I. D., Khar’kiv A. D. Lithospheric mantle of the Yakutian kimberlite province. Moscow: Nauka. 1988. — 287 p. (In Russian)
Khazan Y. Melt segregation and matrix compaction: The mush continuity equation, compaction/segregation time, implications // Geophys. J. Int. 2010. V. 183. P. 601—610.
Khazan Y. Aryasona O. V. Melt segregation inside a partially molten zone: Theory, numerical models, implications // Izvestiya, Physics of the Solid Earth. 2011. Vol. 47, No. 5. P. 425—439.
Kaminsky F. V., Feldman A. A., Varlamov V. A., Boyko A. N., Olofinsky L.N., Shofman I.L. Vaganov V. I. Prognostication of primary diamond deposits // J. Geochem. Exploration. 1995. V. 53. P. 167—182.